El
problema consiste en encontrar los valores desconocidos de las variables
x1,
x2 y
x3 que satisfacen las tres ecuaciones.
El problema de los sistemas lineales de ecuaciones es uno de los más antiguos de la matemática y tiene una infinidad de aplicaciones, como en
procesamiento digital de señales,
análisis estructural, estimación, predicción y más generalmente en
programación lineaEn general, un sistema con m ecuaciones lineales y n incógnitas puede ser escrito en forma normal como:
Donde

son las incógnitas y los números
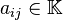
son los coeficientes del sistema sobre el cuerpo
![\mathbb{K}\ [= \R, \mathbb{C}, \dots]](http://upload.wikimedia.org/math/d/d/1/dd172d7f353ca18a891dda59a0d44cc5.png)
. Es posible reescribir el sistema separando con coeficientes con notación matricial:
Si representamos cada matriz con una única letra obtenemos:
Donde
A es una
matriz m por
n,
x es un vector columna de longitud
n y
b es otro vector columna de longitud
m. El sistema de eliminación de Gauss-Jordan se aplica a este tipo de sistemas, sea cual sea el
cuerpo del que provengan los coeficientes.
[editar]Sistemas lineales reales
En esta sección se analizan las propiedades de los sistemas de ecuaciones lineales sobre el cuerpo

, es decir, los sistemas lineales en los cuales los coeficientes de las ecuaciones son
números reales.
[editar]Representación gráfica

La intersección de dos
planosque no son paralelos ni coincidentes es una
recta.
Un sistema con

incógnitas se puede representar en el
n-espacio correspondiente.
En los sistemas con 2 incógnitas, el universo de nuestro sistema será el
plano bidimensional, mientras que cada una de las ecuaciones será representada por una
recta, si es lineal, o por una
curva, si no lo es. La solución será el
punto (o
línea) donde se intersequen todas las rectas y curvas que representan a las ecuaciones. Si no existe ningún punto en el que se intersequen al mismo tiempo todas las líneas, el sistema es incompatible, o lo que es lo mismo, no tiene solución.
En el caso de un sistema con 3 incógnitas, el universo será el espacio tridimensional, siendo cada ecuación un plano dentro del mismo. Si todos los planos intersecan en un único punto, las coordenadas de este serán la solución al sistema. Si, por el contrario, la intersección de todos ellos es una recta o incluso un plano, el sistema tendrá infinitas soluciones, que serán las coordenadas de los puntos que forman dicha línea o superficie.
Para sistemas de 4 ó más incógnitas, la representación gráfica no existe, por lo que dichos problemas no se enfocan desde esta óptica.
[editar]Tipos de sistemas
Los sistemas de ecuaciones se pueden clasificar según el número de soluciones que pueden presentar. De acuerdo con ese caso se pueden presentar los siguientes casos:
- Sistema compatible si tiene solución, en este caso además puede distinguirse entre:
- Sistema compatible determinado cuando tiene una única solución.
- Sistema compatible indeterminado cuando admite un conjunto infinito de soluciones.
- Sistema incompatible si no tiene solución.
Quedando así la clasificación:
Los sistemas incompatibles geométricamente se caracterizan por (hiper)planos o rectas que se cruzan sin cortarse. Los sistemas compatibles determinados se caracterizan por un conjunto de (hiper)planos o rectas que se cortan en un único punto. Los sistemas compatibles indeterminados se caracterizan por (hiper)planos que se cortan a lo largo de una recta [o más generalmente un hiperplano de dimensión menor]. Desde un punto de vista algebraico los sistemas compatibles determinados se caracterizan porque el
determinante de la matriz es diferente de cero:
[editar]Sistemas compatibles indeterminados
Un sistema sobre un cuerpo K es compatible indeterminado cuando posee un número infinito de soluciones. Por ejemplo, el siguiente sistema:
Tanto la primera como la segunda ecuación se corresponden con la recta cuya pendiente es
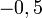
y que pasa por el punto

, por lo que ambas intersecan en todos los puntos de dicha recta. El sistema es compatible por haber solución o intersección entre las rectas, pero es indeterminado al ocurrir esto en infinitos puntos.
- En este tipo de sistemas, la solución genérica consiste en expresar una o más variables como función matemática del resto. En los sistemas lineales compatibles indeterminados, al menos una de sus ecuaciones se puede hallar como combinación lineal del resto, es decir, es linealmente dependiente.
- Una condición necesaria para que un sistema sea compatible indeterminado es que el determinante de la matriz del sistema sea cero (y por tanto uno de sus autovalores será 0):
- De hecho, de las dos condiciones anteriores se desprende, que el conjunto de soluciones de un sistema compatible indeterminado es un subespacio vectorial. Y la dimensión de ese espacio vectorial coincidirá con la multiplicidad geométrica del autovalor cero.
[editar]Sistemas incompatibles
De un sistema se dice que es incompatible cuando no presenta ninguna solución. Por ejemplo, supongamos el siguiente sistema:
Las ecuaciones se corresponden gráficamente con dos rectas, ambas con la misma pendiente, Al ser
paralelas, no se cortan en ningún punto, es decir, no existe ningún valor que satisfaga a la vez ambas ecuaciones.
Matemáticamente un sistema de estos es incompatible cuando el rango de la matriz del sistema es inferior al rango de la matriz ampliada. Una condición necesaria para que esto suceda es que el determinante de la matriz del sistema sea cero:
[editar]Métodos de solución a sistemas de ecuaciones lineales
[editar]Sustitución
El método de sustitución consiste en despejar en una de las ecuaciones cualquier incógnita, preferiblemente la que tenga menor coeficiente, para, a continuación, sustituirla en otra ecuación por su valor.
En caso de sistemas con más de dos incógnitas, la seleccionada debe ser sustituida por su valor equivalente en todas las ecuaciones excepto en la que la hemos despejado. En ese instante, tendremos un sistema con una ecuación y una incógnita menos que el inicial, en el que podemos seguir aplicando este método reiteradamente. Por ejemplo, supongamos que queremos resolver por sustitución este sistema:
En la primera ecuación, seleccionamos la incógnita

por ser la de menor coeficiente y que posiblemente nos facilite más las operaciones, y la despejamos, obteniendo la siguiente ecuación.
El siguiente paso será sustituir cada ocurrencia de la incógnita

en la otra ecuación, para así obtener una ecuación donde la única incógnita sea la

.
Al resolver la ecuación obtenemos el resultado
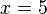
, y si ahora sustituimos esta incógnita por su valor en alguna de las ecuaciones originales obtendremos

, con lo que el sistema queda ya resuelto.
El método de igualación se puede entender como un caso particular del método de sustitución en el que se despeja la misma incógnita en dos ecuaciones y a continuación se igualan entre sí la parte derecha de ambas ecuaciones.
Tomando el mismo sistema utilizado como ejemplo para el método de sustitución, si despejamos la incógnita

en ambas ecuaciones nos queda de la siguiente manera:
Como se puede observar, ambas ecuaciones comparten la misma parte izquierda, por lo que podemos afirmar que las partes derechas también son iguales entre sí.
Una vez obtenido el valor de la incógnita

, se substituye su valor en una de las ecuaciones originales, y se obtiene el valor de la

.
La forma más fácil de tener el método de sustitución es realizando un cambio para despejar x después de averiguar el valor de la y.
Este método suele emplearse mayoritariamente en los sistemas lineales, siendo pocos los casos en que se utiliza para resolver sistemas no lineales. El procedimiento, diseñado para sistemas con dos ecuaciones e incógnitas, consiste en transformar una de las ecuaciones (generalmente, mediante
productos), de manera que obtengamos dos ecuaciones en la que una misma incógnita aparezca con el mismo coeficiente y distinto signo. A continuación, se suman ambas ecuaciones produciéndose así la reducción o cancelación de dicha incógnita, obteniendo así una ecuación con una sola incógnita, donde el método de resolución es simple.
Por ejemplo, en el sistema:
No tenemos más que multiplicar la primera ecuación por
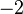
para poder cancelar la incógnita

. Al multiplicar, dicha ecuación nos queda así:
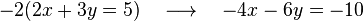
Si sumamos esta ecuación a la segunda del sistema original, obtenemos una nueva ecuación donde la incógnita

ha sido reducida y que, en este caso, nos da directamente el valor de la incógnita

:


El siguiente paso consiste únicamente en sustituir el valor de la incógnita

en cualquiera de las ecuaciones donde aparecían ambas incógnitas, y obtener así que el valor de

es igual a:

[editar]Método gráfico
Consiste en construir la gráfica de cada una de las ecuaciones del sistema. El método (manualmente aplicado) solo resulta eficiente en el plano cartesiano, es decir para un espacio de dimensión 2.
El proceso de resolución de un sistema de ecuaciones mediante el método gráfico se resuelve en los siguientes pasos:
- Se despeja la incógnita (y) en ambas ecuaciones.
- Se construye para cada una de las dos ecuaciones de primer grado obteniendo la tabla de valores correspondientes.
- Se representan gráficamente ambas rectas en los ejes coordenados.
- En este último paso hay tres posibilidades:
- Si ambas rectas se cortan, las coordenadas del punto de corte son los únicos valores de las incógnitas (x,y). "Sistema compatible determinado".
- Si ambas rectas son coincidentes, el sistema tiene infinitas soluciones que son las respectivas coordenadas de todos los puntos de esa recta en la que coinciden ambas. «Sistema compatible indeterminado».
- Si ambas rectas son paralelas, el sistema no tiene solución.
[editar]Método de Gauss
El método de eliminación de Gauss o simplemente método de Gauss consiste en convertir un sistema lineal de n ecuaciones con nincognitas, en uno escalonado, en el que la primera ecuación tiene n incógnitas, la segunda ecuación tiene n - 1 incógnitas, ..., hasta la última ecuación, que tiene 1 incógnita. De esta forma, será fácil partir de la última ecuación e ir subiendo para calcular el valor de las demás incógnitas.
| [Mostrar] Ejemplo de eliminación de Gauss |
[editar]Eliminación de Gauss-Jordan
Una variante de este método, denominada
eliminación de Gauss-Jordan, es un método aplicable únicamente a los sistemas lineales de ecuaciones, y consistente en triangular la
matriz aumentada del sistema mediante transformaciones elementales, hasta obtener ecuaciones de una sola incógnita, cuyo valor será igual al coeficiente situado en la misma fila de la matriz. Este procedimiento es similar al anterior de reducción, pero ejecutado de manera reiterada y siguiendo un cierto orden algorítmico.
| [Mostrar] Ejemplo de eliminación de Gauss-Jordan |
[editar]Regla de Cramer
La regla de Cramer da una solución para sistemas compatibles determinados en términos de
determinantes y adjuntos dada por:
Donde Aj es la matriz resultante de remplazar la j-ésima columna de A por el vector columna b. Para un sistema de dos ecuaciones y dos incógnitas:
La regla de Cramer da la siguiente solución:
Nota: Cuando en la determinante original det(A) el resultado es 0, el sistema indica múltiples o sin coincidencia.
[editar]Algoritmos numéricos
La
eliminación de Gauss-Jordan es un algoritmo numérico usado para una gran cantidad de casos específicos, aunque posterioremente se han desarrollado algoritmos alternativos mucho más eficientes. La mayoría de estos algoritmos mejorados tienen una complejidad computacional de
O(n²) (donde
n es el número de ecuaciones del sistema). Algunos de los métodos más usados son:
Cuando consideramos ecuaciones lineales cuyas soluciones son números racionales, reales o complejos o más generalmente un cuerpo

, la solución puede encontrarse mediante
Regla de Cramer. Para sistemas de muchas ecuaciones la regla de Cramer puede ser computacionalmente más costosa y suelen usarse otros métodos más "económicos" en número de operaciones como la
eliminación de Gauss-Jordan y la
descomposición de Cholesky. Existen también métodos indirectos (basados en iteraciones) como el
método de Gauss-Seidel.
Si el cuerpo es
infinito (como es el caso de los números
reales o
complejos), entonces solo puede darse una de las tres siguientes situaciones:
- el sistema no tiene solución (en dicho caso decimos que el sistema está sobredeterminado o que es incompatible)
- el sistema tiene una única solución (el sistema es compatible determinado)
- el sistema tiene un número infinito de soluciones (el sistema es compatible indeterminado).
Anteriormente has usado los símbolos “>” (mayor que), “<” (menor que), “≥” (mayor o igual que) y “≤” (menor o igual que) para describir como es la relación entre un número y otro. Por ejemplo: 4 > -1 para señalar que 4 es mayor que -1, -2 < 3 para señalar que -2 es menor que 3 y -3 < -1 para señalar que -3 es menor que -1. Estos ejemplos se conocen como desigualdades.
Podemos usar la recta numérica para visualizar estas desigualdades.
Observa que:
4 > -1, porque 4 está a la derecha de -1 en la recta numérica.
-2 < 3, porque -2 está a la izquierda de 3 en la recta numérica
-3 < -1, porque -3 está a la izquierda de -1 en la recta numérica
0 > -4, porque 4 está a la derecha de 0 en la recta numérica
Una inecuación lineal es una expresión matemática que describe cómo se relacionan entre sí dos expresiones lineales. Por ejemplo: 3 + 5x ≥ 18; -2(x + 3) < -9.
La solución de una inecuación lineal se puede representar haciendo uso de intervalos en la recta numérica, la cual contiene infinito números reales.
Para resolver inecuaciones lineales hacemos uso de las siguientes propiedades:
- Para todo número real a, b y c, si a < b entonces: a + c < b + c y a – c < b – c.
- Para todo número real a, b y c, donde c > 0 y a < b, entonces:
3. Para todo número real a, b y c, donde c < 0, si a < b, entonces:
Ejemplos para discusión: Resuelve las siguientes inecuaciones lineales y representa la solución en la recta numérica.
1) x + 5 < 3
2) 3x + 2(x – 4) > 4x
3) 5x – 7 ≤ 2x + 8
4) 3x + 8 ≥ 5x
Inecuaciones complejas
Las inecuaciones complejas son aquellas que consisten de dos inecuaciones que están unidas por la conjunción “ó” (“or”) ó por la conjunción “y” (“and”).
Ejemplos: Resuelve para x y representa la solución en la recta numérica:
1) 3x + 2 > 14 ó 2x – 1 < -7
2) 5x – 1 ≥ - 4 y 3x – 4 < 8
3) -3x + 1 ≤ 7 ó 3x + 1 ≤ -4
4) -4 ≤ 3x – 1 ≤ 5
 Práctica: Resuelve las siguientes inecuaciones lineales e inecuaciones compuestas (ejercicios 4 y 5) y representa la solución en la recta numérica.
Práctica: Resuelve las siguientes inecuaciones lineales e inecuaciones compuestas (ejercicios 4 y 5) y representa la solución en la recta numérica.
1) 5x + 2 < 4 – x
2) 7(x – 3) ≥ 4(1 + 2x)
4) 3x – 4 < -1 ó 2x + 3 ≥ 13
5) 3x + 6 > -6 y 4x + 5 < 1
6) -4 ≤ 3x + 1 < 5
Prof. Nilsa Toro
GEMA 1200
 Ejercicios adicionales: Resuelve las siguientes inecuaciones y dibuja la gráfica del conjunto solución:
Ejercicios adicionales: Resuelve las siguientes inecuaciones y dibuja la gráfica del conjunto solución:
1) -2z < 10
|
7) 3x – 4 < x + 8
|
2) 3a – 1 ≥ 14
|
8) 2p + 5 ≥ 3p - 8
|
3) 3(x – 2) + 5x > 22
|
|
4) 2m + 5 < 3m – 8
|
10) 2 ≤ 5x + 3 < 15
|
5) y + 4 ≤ 3y – 1
|
11) 10 < 3p – 4 < 18
|
|
|
|

 , luego,
, luego, 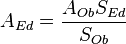









 : es el error que hemos cometido al calcular la altura del edificio.
: es el error que hemos cometido al calcular la altura del edificio. : es el error de medida de la sombra del edificio.
: es el error de medida de la sombra del edificio. : es el error de medida en la altura del objeto.
: es el error de medida en la altura del objeto. : es el error de medida en la sombra del objeto.
: es el error de medida en la sombra del objeto.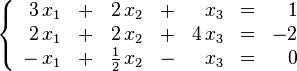
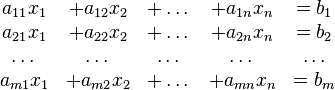
 son las incógnitas y los números
son las incógnitas y los números 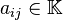 son los coeficientes del sistema sobre el cuerpo
son los coeficientes del sistema sobre el cuerpo ![\mathbb{K}\ [= \R, \mathbb{C}, \dots]](http://upload.wikimedia.org/math/d/d/1/dd172d7f353ca18a891dda59a0d44cc5.png) . Es posible reescribir el sistema separando con coeficientes con notación matricial:
. Es posible reescribir el sistema separando con coeficientes con notación matricial: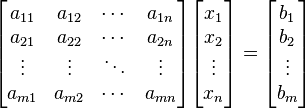
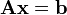
 , es decir, los sistemas lineales en los cuales los coeficientes de las ecuaciones son
, es decir, los sistemas lineales en los cuales los coeficientes de las ecuaciones son 
 incógnitas se puede representar en el
incógnitas se puede representar en el 
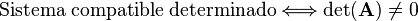

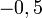 y que pasa por el punto
y que pasa por el punto  , por lo que ambas intersecan en todos los puntos de dicha recta. El sistema es compatible por haber solución o intersección entre las rectas, pero es indeterminado al ocurrir esto en infinitos puntos.
, por lo que ambas intersecan en todos los puntos de dicha recta. El sistema es compatible por haber solución o intersección entre las rectas, pero es indeterminado al ocurrir esto en infinitos puntos.

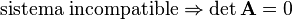

 por ser la de menor coeficiente y que posiblemente nos facilite más las operaciones, y la despejamos, obteniendo la siguiente ecuación.
por ser la de menor coeficiente y que posiblemente nos facilite más las operaciones, y la despejamos, obteniendo la siguiente ecuación.
 .
.
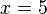 , y si ahora sustituimos esta incógnita por su valor en alguna de las ecuaciones originales obtendremos
, y si ahora sustituimos esta incógnita por su valor en alguna de las ecuaciones originales obtendremos  , con lo que el sistema queda ya resuelto.
, con lo que el sistema queda ya resuelto.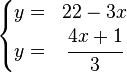


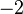 para poder cancelar la incógnita
para poder cancelar la incógnita 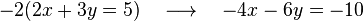






 , la solución puede encontrarse mediante
, la solución puede encontrarse mediante 